9 Centrálna limitná veta

Normálne rozdelenie hrá prekvapivo dôležitú úlohu v teórii pravdepodobnosti a v štatistike. Ukazuje sa, že aritmetický priemer z nezávislých, ale rovnako rozdelených náhodných premenných, pokiaľ je počítaný z dostatočne veľkého množstva premenných, sa správa ako normálne rozdelená náhodná premenná.

9.1 Konvergencia podľa distribúcie

V minulej kapitole sme si predstavili jeden zo spôsobov, ako sa môže postupnosť náhodných premenných blížiť k nejakej náhodnej premennej, konkrétne konvergenciu podľa pravdepodobnosti. Existuje aj iný spôsob. Niekedy chceme uvažovať situáciu, že pravdepodobnostné správnanie prvkov postupnosti náhodných premenných sa stále viacej a viacej podobá na pravdepodobnostné správanie akejsi limitnej náhodnej premennej.

Hovoríme, že postupnosť náhodných premenných \(\{X_i\}_{i=1}^{\infty}\) konverguje podľa distribúcie k náhodnej premennej \(X\), ak platí pre všetky body \(x\) spojitosti funkcie \(F_X\):

\[\lim_{n \rightarrow \infty}F_{X_n}(x) = F_X(x),\] Označujeme \(X_n \rightarrow_D X.\)

Platí \[X_n \rightarrow_P X \implies X_n \rightarrow_D X.\]

Dôkaz. Nakoľko platí \(\{ X_n \leq x\} \subset \{ X \leq x + \epsilon\} \cup \{|X-X_n| > \epsilon\}\) (lebo ak platí \(X_n \leq x\) a \(X > x + \epsilon\), potom nutne aj \(|X-X_n| > \epsilon\)), dostávame: \[\begin{eqnarray*} P(X_n \leq x) &\leq& P(X \leq x + \epsilon) + P(|X_n - X|>\epsilon). \end{eqnarray*}\] Podobnou úvahou dostaneme

\[\begin{eqnarray*} P(X \leq x-\epsilon) &\leq& P(X_n \leq x) + P(|X_n - X|>\epsilon). \end{eqnarray*}\]

Preto platí

\[P(X \leq x-\epsilon) - P(|X_n - X|>\epsilon) \leq P(X_n \leq x) \leq P(X \leq x + \epsilon) + P(|X_n - X|>\epsilon).\]

Ak aplikujeme operátor limity na tieto nerovnosti, spolu s využitím definície konvergencie podľa pravdepodobnosti dostávame

\[F_{X}(x-\epsilon) \leq \lim_{n \rightarrow \infty}P(X_n \leq x) \leq F_{X}(x+\epsilon),\] a tieto nerovnosti platia pre akékoľvek \(\epsilon.\)

V bode spojitosti \(F_X\) platí \(\lim_{\epsilon \rightarrow 0}F_{X}(x-\epsilon) = \lim_{\epsilon \rightarrow 0}F_{X}(x+\epsilon) = F_X(x),\) a preto \(\lim_{n \rightarrow \infty}P(X_n \leq x) = F_X(x)\), čo sme chceli ukázať.

9.2 Centrálna limitná veta

Majme postupnosť nezávislých a rovnako rozdelených náhodných premenných \(X_1, X_2, X_3, \dots\) s konečnou strednou hodnotou \(\mu\) a konečnou varianciou \(\sigma^2.\) Potom platí

\[\sqrt{n}\frac{\bar{X}_n - \mu}{\sigma} \rightarrow_D Z,\]

kde \(Z \sim \text{N}(0,1).\)

Alternatívnym zápisom je, že ak označíme \(Y_n = \sqrt{n}\frac{\bar{X}_n - \mu}{\sigma},\) potom

\[\forall x \in \mathbb{R}: \lim_{n \rightarrow \infty}F_{Y_n}(x) = \Phi(x).\]

Dôkaz je nad rámec tohoto kurzu, a preto ho vynechávame.

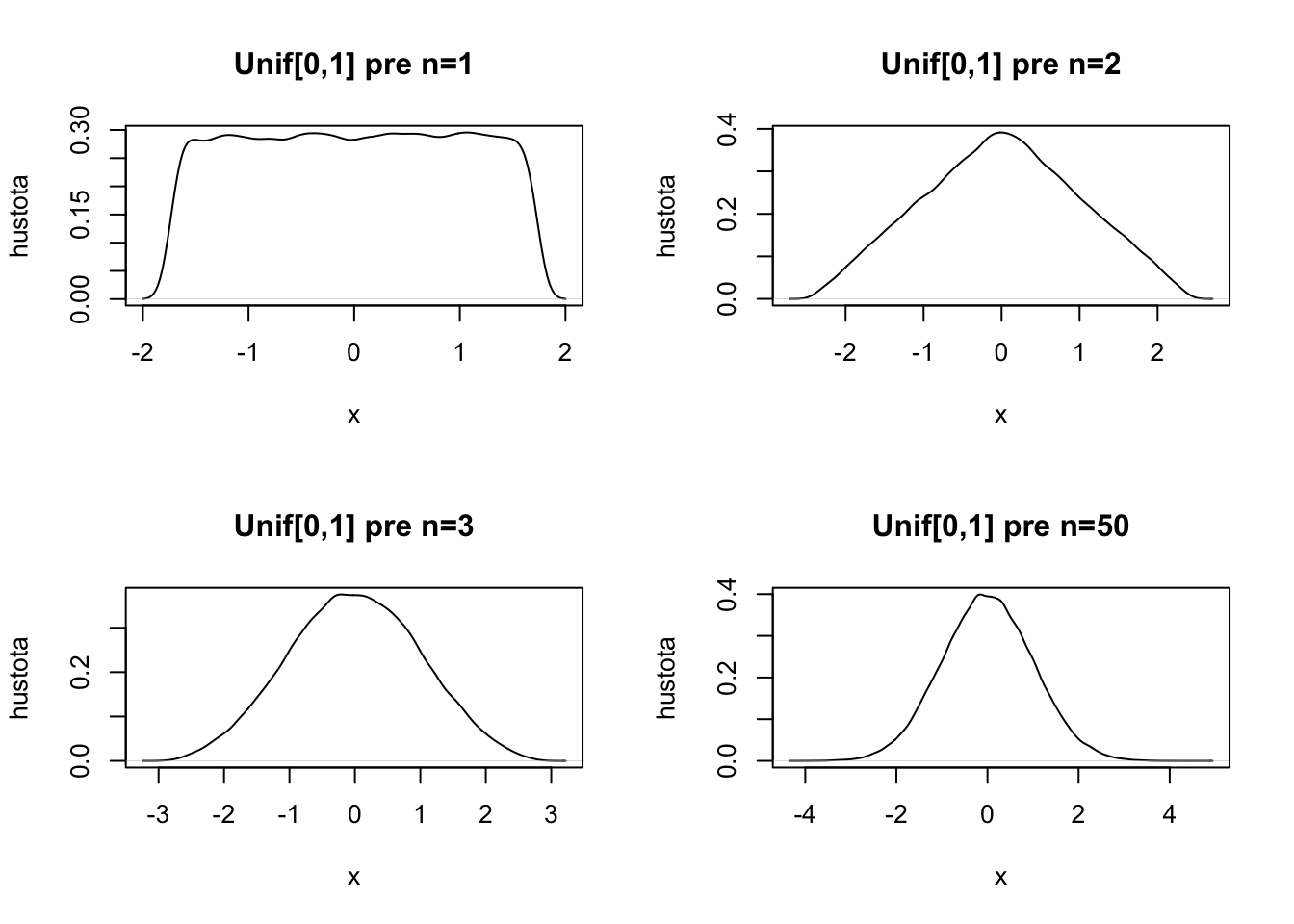
Tu je ilustrácie pre rovnomerné rozdelenie. Ide o obrázky odhadov funkcie hustoty. Napriek veľkému množstvu simulácií nie sú úplne hladké, viacej o takýchto odhadoch hustôt sa naučíme na druhom kurze regresie.

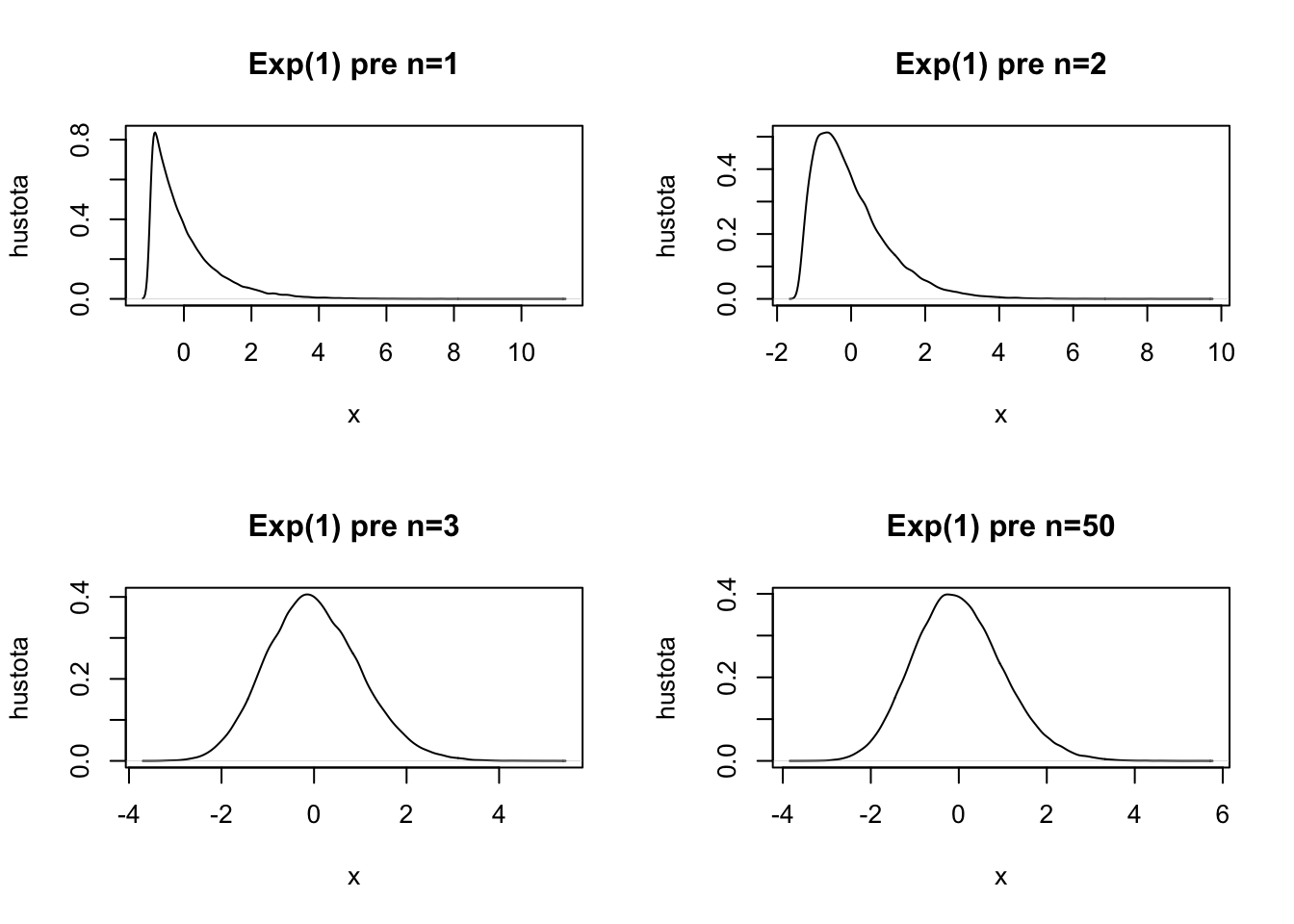
Tu pre exponenciálne rozdelenie:

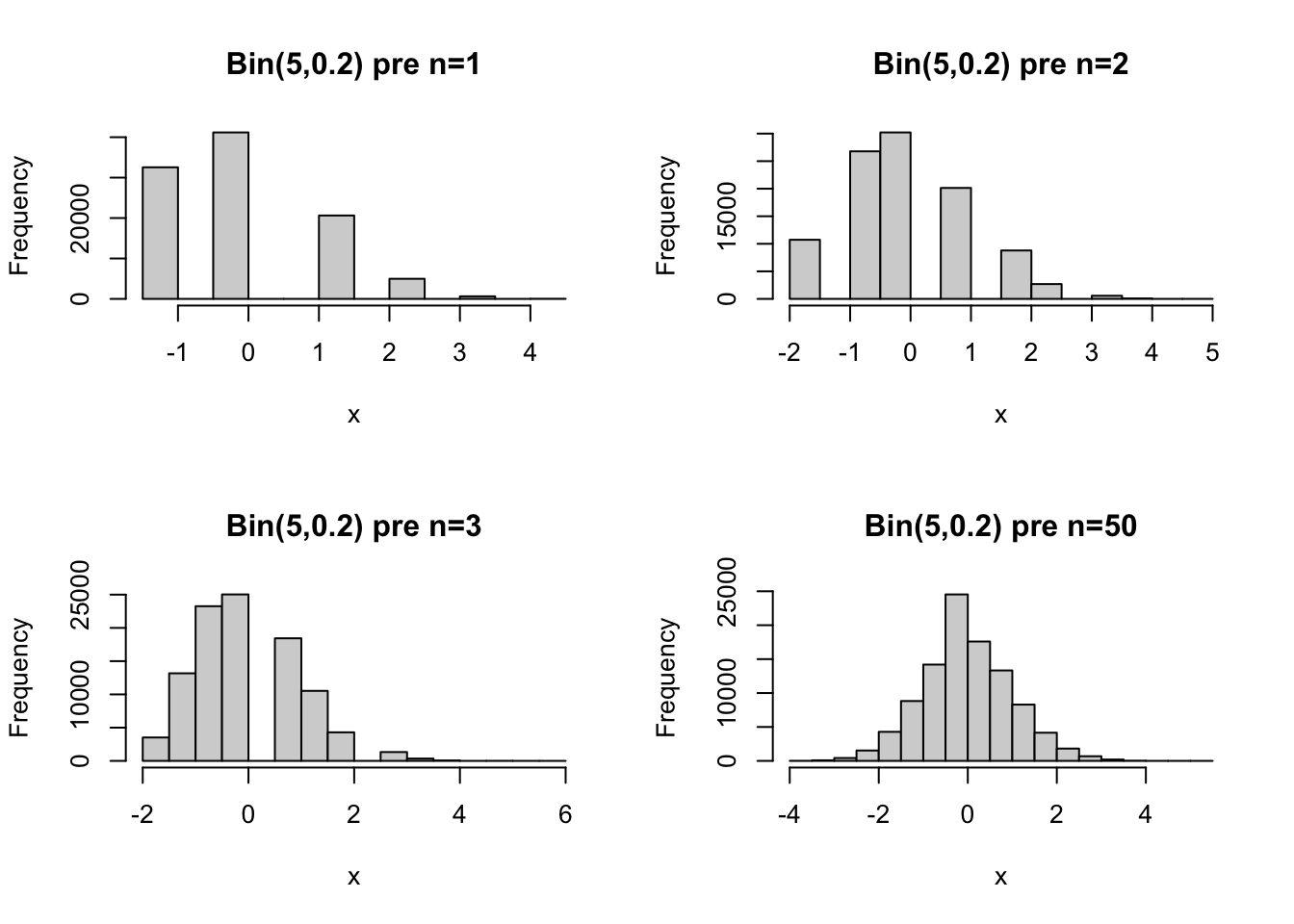
A tu pre binomické rozdelenie:

Animácia nižšie ilustruje Centrálnu limitnú vetu. Čím väčšia je vzorka, tým bližšie je centrovaný a vyškálovaný aritmetický priemer bližšie normovanému normálnemu (\(N(0,1)\)) rozdeleniu.

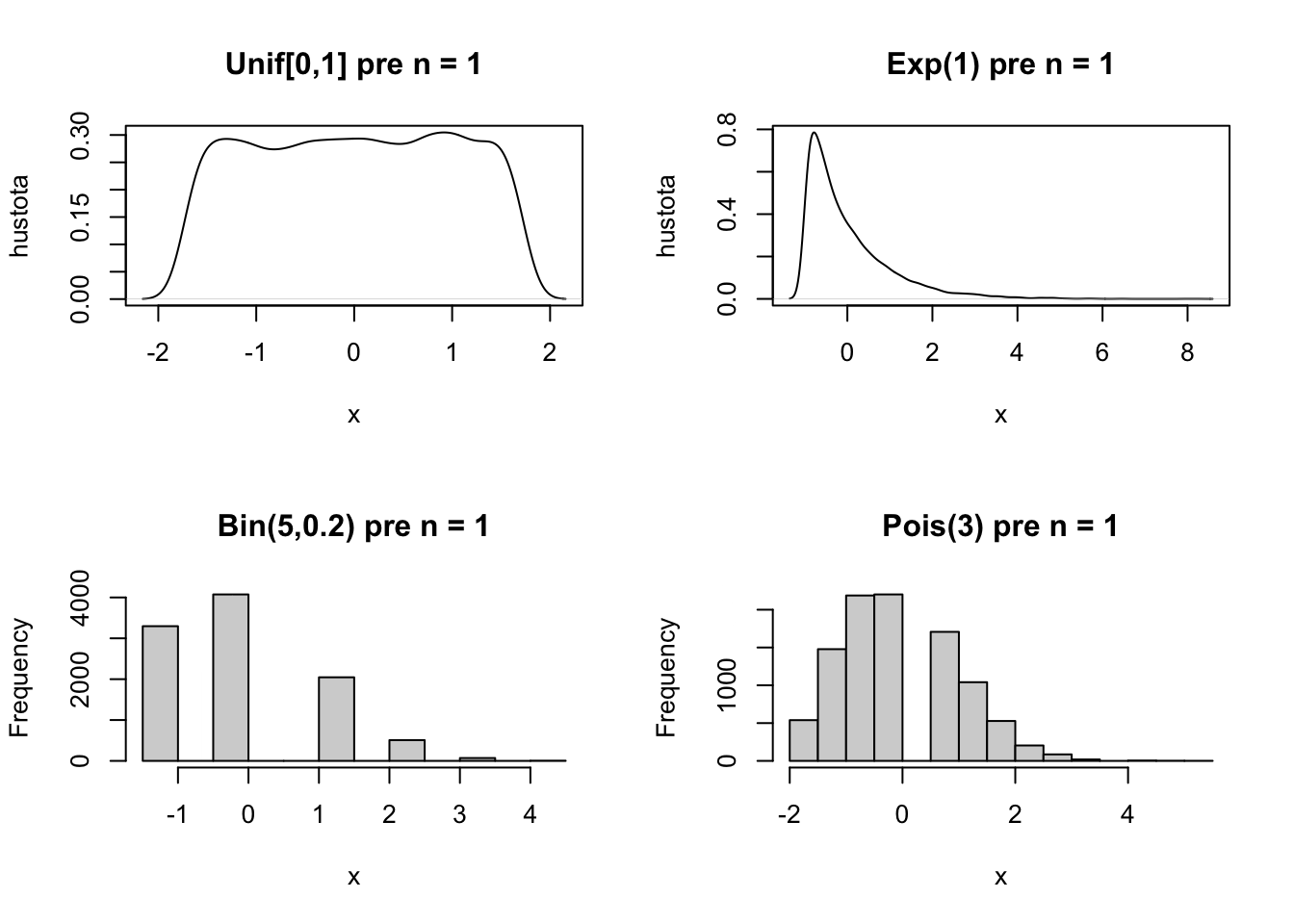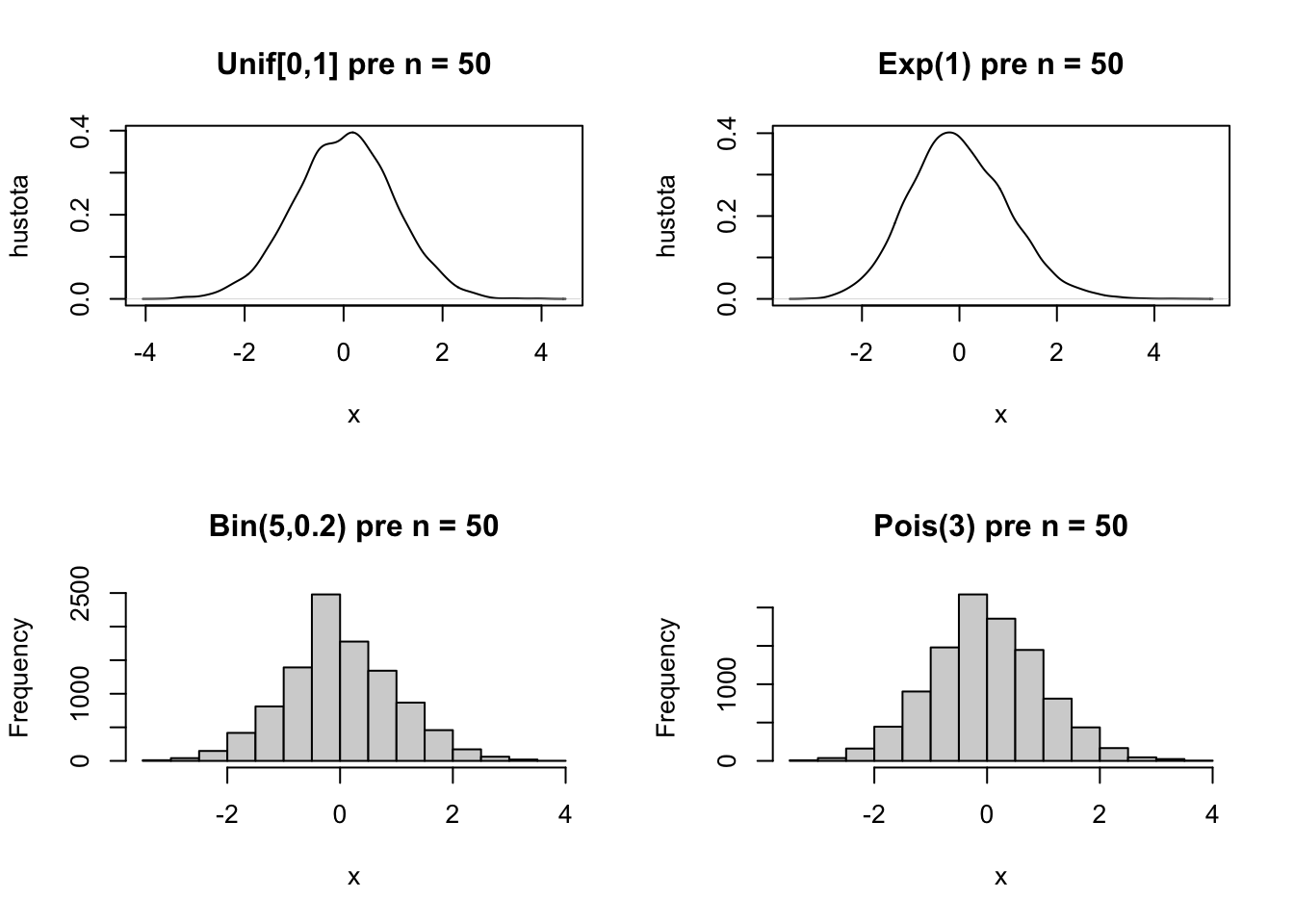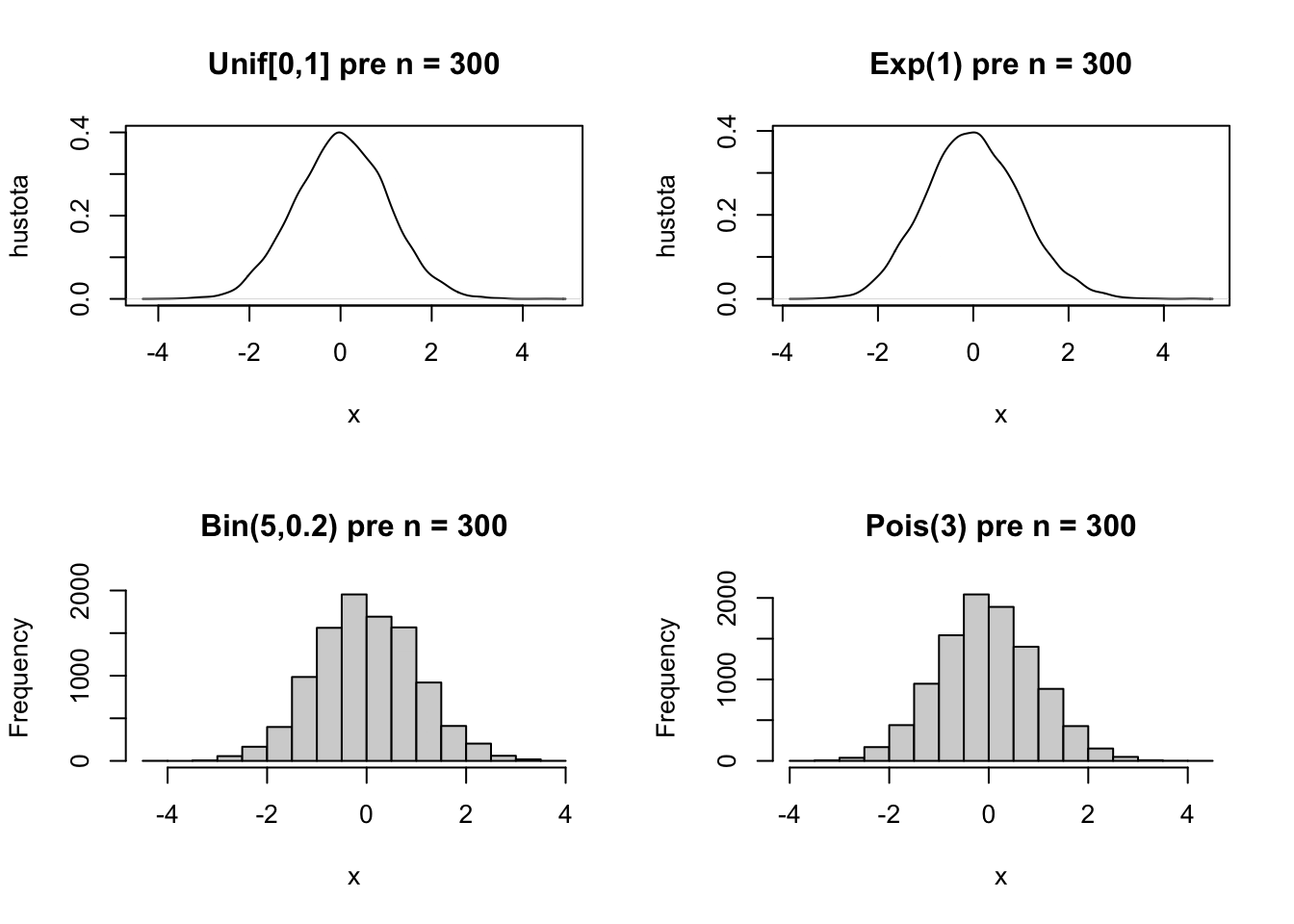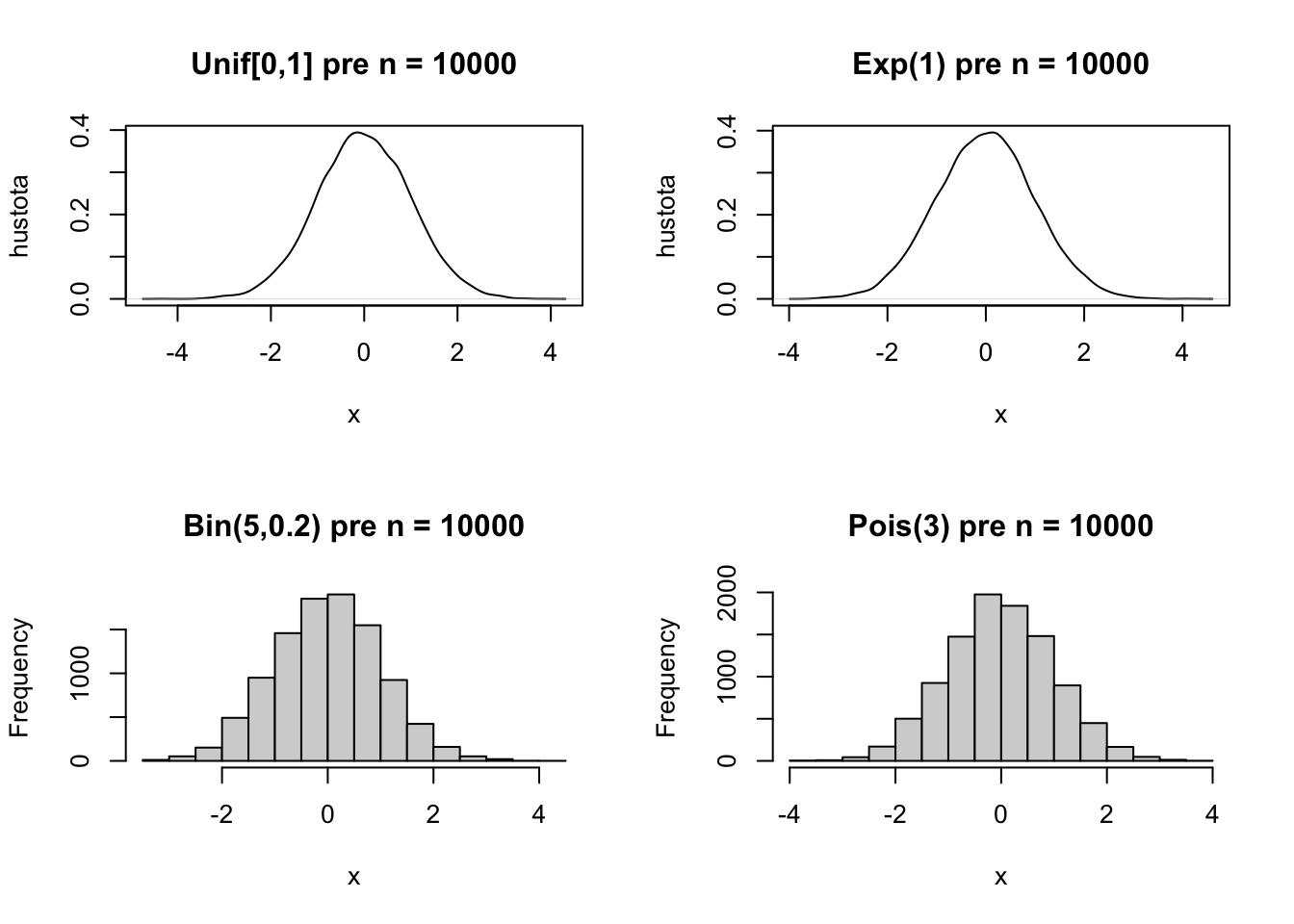
Toto má dôležité praktické dôsledky. My vôbec nemusíme vedieť, aké má nejaká náhodná pravdepodobnostné rozdelenie. Ale vieme, že priemer nezávislých náhodných premenných sa už bude správať systematicky(!). Toto je veľmi všeobecný výsledok. Na tomto poznatku je založených mnoho štatistických testov.

Príklad 9.1 Hádžeme férovou mincou 900 krát. Ideme aproximovať pravdepodobnosť, že uvidíme viacej ako 495 hláv. Každý hod mincou \(X_i \sim \text{Bern}(0.5)\) a \(\text{E}[X_i] = 0.5, \text{Var}[X_i] = 0.25.\)

Preto

\[\begin{eqnarray*} P\left(\sum_{i=1}^{900} X_i > 495\right)&=& P\left(\frac{\sum_{i=1}^{900} X_i}{900} > \frac{495}{900}\right) \\ &=& P\left(\bar{X}_n - 0.5 > \frac{495}{900} -0.5\right)\\ &=& P\left(\frac{\bar{X}_n - 0.5}{0.5} > \frac{\frac{495}{900} -0.5}{0.5}\right)\\ &=& P\left(\sqrt{900}\frac{\bar{X}_n - 0.5}{0.5} > \sqrt{900}\frac{\frac{495}{900} -0.5}{0.5}\right)\\ &=& P\left(\sqrt{900}\frac{\bar{X}_n - 0.5}{0.5} > 30\frac{\frac{495}{900} -0.5}{0.5}\right)\\ &=& P\left(\sqrt{900}\frac{\bar{X}_n - 0.5}{0.5} > 3\right)\\ &\approx& 1-\Phi(3) = 0.0013 \end{eqnarray*}\]

Princíp výpočtu takýchto aproximácií je vždy rovnaký. Začneme s tým, čo chceme vypočítať a ekvivalentnými úpravami to prevedieme na formuláciu CLV.

Príklad 9.2 Majme nezávislé \(X_1, X_2, \cdots X_{12}\) kde \(X_i \sim \text{Unif}[0,1].\) Pomocou CLV aproximujte \(P(|\bar{X}_n - 0.5| \leq 0.1).\) \[\begin{eqnarray*} P(|\bar{X}_n - 0.5| \leq 0.1) &=& P(\sqrt{12}(\bar{X}_n - 0.5)| \leq \sqrt{12}\cdot 0.1)\\ &=& P\left(\left|\sqrt{12}\frac{\bar{X}_n - 0.5}{\sqrt{\frac{1}{12}}}\right| \leq \sqrt{12}\frac{0.1}{\sqrt{\frac{1}{12}}}\right)\\ &=& P\left(\left|\sqrt{12}\frac{\bar{X}_n - 0.5}{\sqrt{\frac{1}{12}}}\right| \leq 1.2\right)\\ &\approx& \Phi(1.2) - \Phi(-1.2) = 0.7698. \end{eqnarray*}\]

Využili sme skutočnosť, že \(\sqrt{n}\frac{\bar{X}_n - \mu}{\sigma}\) je približne normovane normálne rozdelená náhodná premenná (\(\text{N}(0,1)\)).

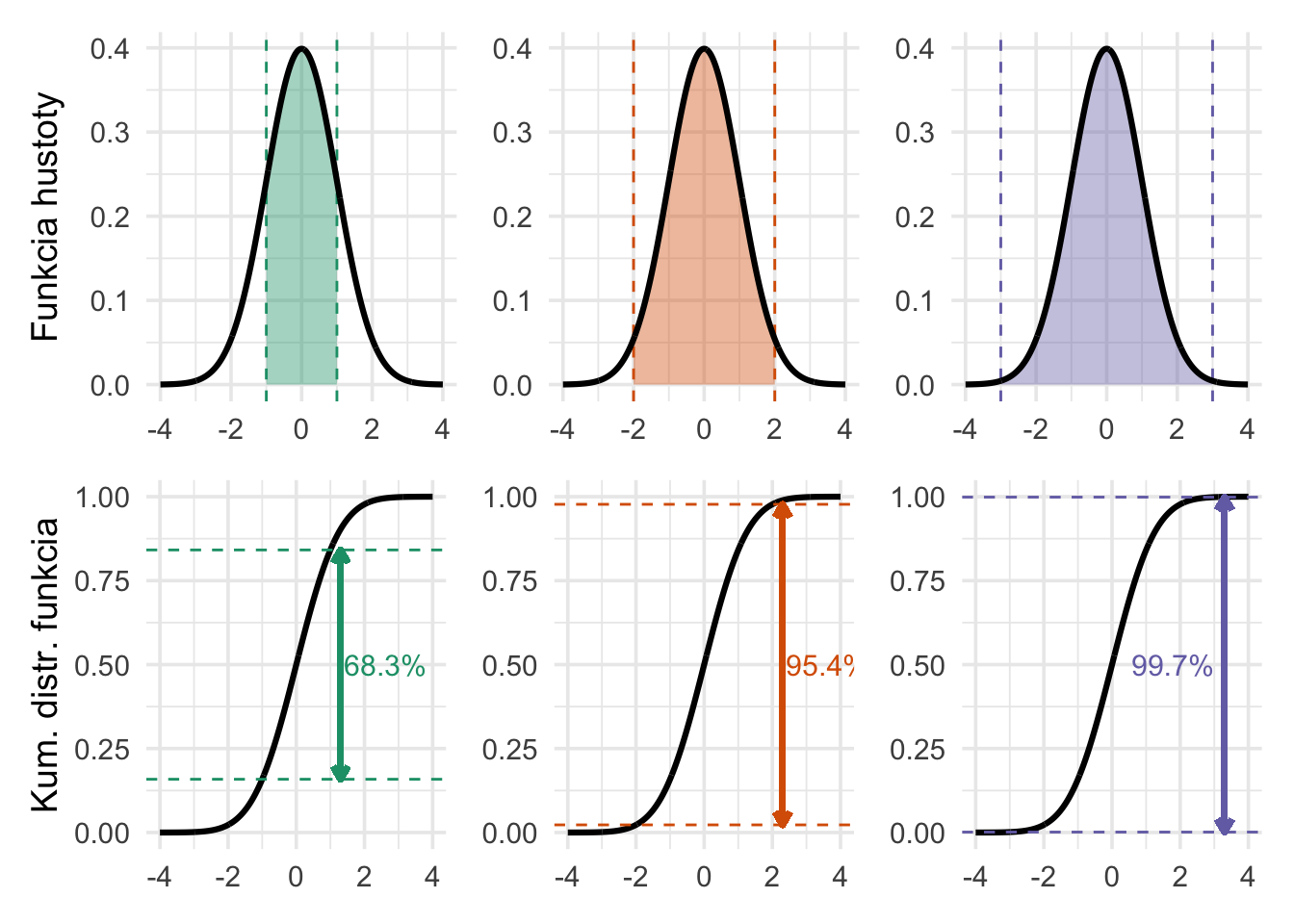
Nasledujúci obrázok vizualizuje tri dôležité hodnoty pre normované normálne rozdelenie.

\[ \color{green} \Phi(1) - \Phi(-1) \approx 0.683, \quad \color{red} \Phi(2) - \Phi(-2) \approx 0.954, \quad \color{purple} \Phi(3) - \Phi(-3) \approx 0.997. \]

Vo výpočtovom prostredí R môžeme na výpočet \(\Phi(1.6)\) môžete použiť funkciu pnorm(1.6) a na výpočet \(\Phi^{-1}(0.75)\) môžete použiť funkciu qnorm(0.75).

V Exceli by to bolo NORM.S.DIST(1.6,TRUE) a NORM.S.INV(0.75).

Naozaj skvelá vizualizácia a vysvetlenie CLT je na tomto videu od 3Blue1Brown.

Tu je zas vysvetelnie, skadiaľ je to číslo \(\pi\) v funkcii hustoty normovaného normálneho rozdelenia. 3Blue1Brown

9.3 Cvičenia

Cvičenie 9.1 Majme postupnosť nezávislých a rovnako rozdelených náhodných premenných \(X_1,X_2,X_3,\cdots\), kde \(X_1 \sim \text{Exp}(1).\)

Aké veľké musí byť \(n\) aby platilo \(P(0.9 \leq \bar{X}_n \leq 1.1)\geq 0.9\) ?

Cvičenie 9.2 Výťah unesie 4tony nákladu. Majme 100 krabíc, každá s priemernou váhou 39kg a so smerodajnou odchýlkou 2kg. Aproximujte pravdepodobnosť, že výťah bude preťažený.

Cvičenie 9.3 Majme postupnosť nezávislých a rovnako rozdelených náhodných premenných \(X_1,X_2,X_3,\cdots\), kde \(\text{E}[X_1] = 200, \text{Var}[X_1]=40, n=100.\)

Aproximujte pomocou CLV hodnotu \(P(190 \leq \bar{X}_n \leq 210)\).

Cvičenie 9.4 Na Deň otvorených dverí príde 100 hostí. Každý hosť si zoberie 0, 1 alebo 2 brožúry o Katedre matematiky s pravdepodobnosťou 1/4, 1/2 a 1/4. Ľudia si brožúry berú nezávisle. Koľko brožúr musíme dať vytlačiť, aby sme si boli na 97% istí, že nebudú chýbať?

Porovnajte výsledky, ktoré dostanete:

aplikovaním Markovovej nerovnosti
pomocou Centrálnej limitnej vety

Cvičenie 9.5 Máme produkt, o ktorého kazivosti vieme, že je 0.1%. V poslednej objednávke, v ktorej bolo 1200ks týchto produktov sme pozorovali 4 chybné produkty, čo sa nám zdá dosť veľa. Aká je pravdepodobnosť, že by sme pozorovali 4 alebo viacej chybných produktov?

Porovnajte výsledky, ktoré dostanete:

aplikovaním Markovovej nerovnosti
priamym výpočtom pomocou Binomického rozdelenia
aproximáciou Binomického rozdelenia pomocou Poissonoveho rozdelenia
aproximáciou pomocou Centrálnej limitnej vety

Cvičenie 9.6 Predstavte, že by ste simulačne chceli odhadnúť obsah tohoto útvaru, ktorý je ohraničený krivkami, ktorých predpis teraz nepoznáme. Budeme uniformne náhodne vyberať \(X\) a \(Y\) a pozerať sa, aká proporcia \((X,Y)\) padne medzi tieto krivky.

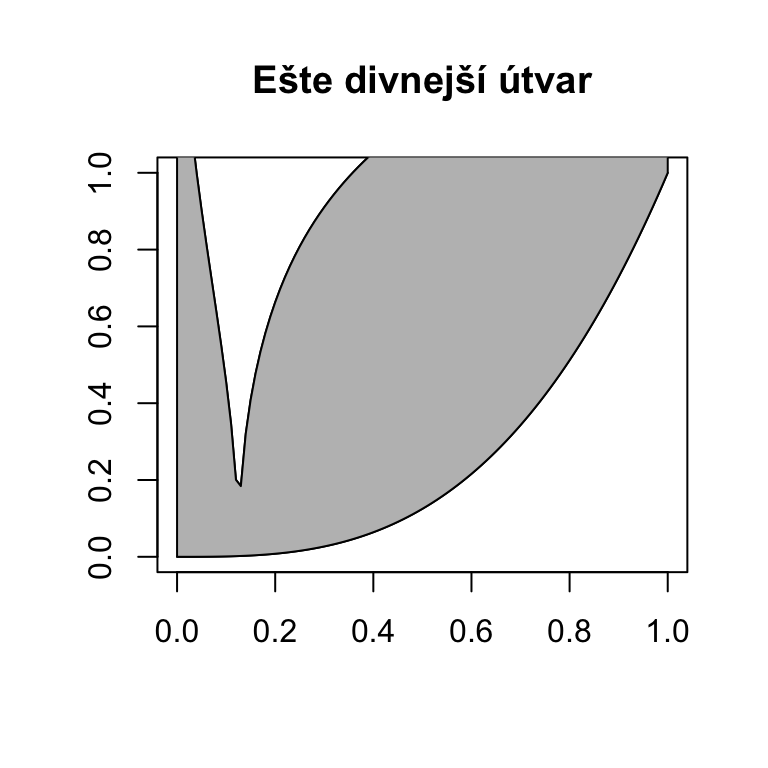
Odhadnite koľko najmenej simulácií by ste potrebovali, aby ste mali zagarantované, že odhadnete skutočný obsah s presnosťou 0.001 s pravdepodobnosťou aspoň \(99.9\%\).

Cvičenie 9.7 V populácii máme \(8.2\%\) farboslepých ľudí. Náhodne vyberieme \(n\) ľudí do prieskumu, pýtame sa ich a predpokladáme, že nám hovoria pravdu.

Aká je pravdepodobnosť, že podiel farboslepých ľudí v našej vzorke sa od reality bude líšiť o viac ako \(2\) percentuálne body, ak vezmeme vzorku \(200\), resp. \(5000\) ľudí? Odpovedzte (obidve)

pomocou Čebyševovej nerovnosti
na základe aproximácie pomocou Centrálnej limitnej vety.

Koľkých ľudí sa musíme opýtať, ak chceme, aby sa s \(90\%\)-tnou istotou podiel farboslepých ľudí v našej vzorke líšil od reality najviac o \(1\) percentuálny bod? Odpovedzte (obidve)

pomocou Čebyševovej nerovnosti
na základe aproximácie pomocou Centrálnej limitnej vety.

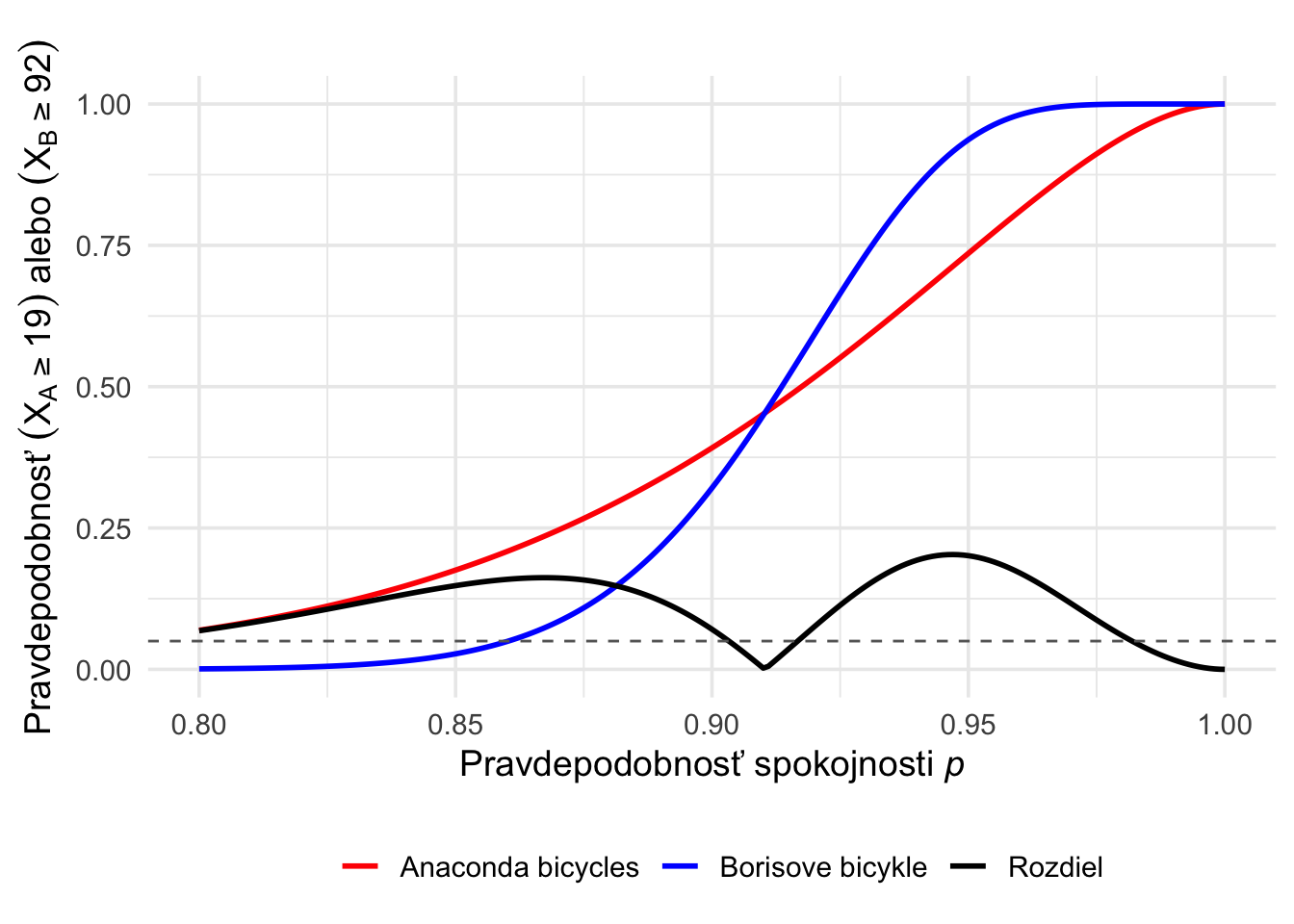
Cvičenie 9.8 Zvažujete kúpu konkrétneho bicykla, ktorý sa predáva v dvoch rôznych obchodoch. Prvý obchod Anaconda bicycles reportuje, že 19 z 20 ľudí bolo s týmto bicyklom spokojných. U druhého obchodu Borisove bicykle bolo 92 z 100 ľudí spokojných. Nech náhodné premenné \(X_A \sim Bin(20,p)\) a \(X_B \sim Bin(100,p)\) označujú počty ľudí spokojných s tými bicyklami v daných obchodoch. Predpokladajme, že informácie o spokojnosti zákazníkov, ktoré pozorujeme nie je systematicky oveľa viacej alebo menej kvalitné, čo kvantifikujeme nasledovným spôsobom

\[|P(X_A \geq 19) - P(X_B \geq 92)| < 0.05.\]

Naviac predpokladajme, že \(p>0.8.\)

Ako veľmi sú ľudia spokojní?

Inými slovami, aké hodnoty pravdepodobnosti \(p\) sú v súlade s týmito predpokladmi?

Cvičenie 9.9 Zo sčítania obyvateľstva vieme, že v populácii máme \(18.4\%\) vysokoškolsky vzdelaných ľudí. Náhodne vyberieme \(n\) ľudí do prieskumu.

Pomocou Čebyševovej nerovnosti odhadnite, aká je pravdepodobnosť, že pomer vysokoškolsky vzdelaných ľudí v našej vzorke sa od reality bude líšiť o viac ako \(2\%\), ak vezmeme vzorku \(100\), resp. \(1000\) ľudí?
Pomocou Čebyševovej nerovnosti odhadnite, koľkých ľudí sa musíme opýtať, ak chceme, aby sa s \(95\%\)-tnou istotou pomer vysokoškolsky vzdelaných ľudí v prieskume líšil od reality najviac o \(2\%\), resp. \(5\%\)?

Cvičenie 9.10 200 ľudí čaká v rade na lístky na koncert. Každý človek v rade si kúpi v priemere 2.3 lístkov zo smerodajnou odchýlkou 2. V sále je 500 voľných miest. Aproximujte pravdepodobosť, že sa každému ujde toľko lístkov, koľko chce. Explicitne pomenujte zjednodušujúce predpoklady, ktoré urobíte.

Cvičenie 9.11 Na pumpe v Hronskej Breznici sa týždenne predá v priemere 50000 litrov benzínu so smerodajnou odchýlkou 10000 litrov. Na začiatku je v zásobníku 74000 litrov a každý týžden je naplánovaná dodávka 47000 litrov.

Aproximujte pravdepodobnosť, že po 11 týždňoch bude v zásobníku menej ako 20000 litrov.
Aká by mala byť plánovaná týždenná dodávka, aby bola pravdepodobnosť, že po 11 týždňoch bude v zásobníku menej ako 20000 litrov menšia ako 0.5%?

Niektoré riešenia

Cvičenie 9.8

Vyjadrím {\(P(X_A \geq 19)\)} a {\(P(X_B \geq 92)\)} a zakreslíme do obrázka. Rozdiel je zaznačený čiernou farbou.

Zadaniu vyhovujú intervaly \([0.904, 0.916]\) a \([0.982, 1].\)

Cvičenie 9.10

200 ľudí čaká v rade na lístky na koncert. Každý človek v rade si kúpi v priemere 2.3 lístkov zo smerodajnou odchýlkou 2. V sále je 500 voľných miest. Aproximujte pravdepodobosť, že sa každému ujde toľko lístkov, koľko chce. Explicitne pomenujte zjednodušujúce predpoklady, ktoré urobíte.

Nech \(X_i\) označuje počet kúpených lístkov pre človek \(i\). Teda \(\text{E}[X_i] = 2.3\) a \(\text{Var}[X_i] = 4.\)

Uvažujeme, že počty kúpených lístkov rôznymi ľudmi sú nezávislé náhodné premenné.

Nech \(S_n = X_1 + \cdots X_{n}\) a \(\bar{X}_n = \frac{X_1 + \cdots X_{n}}{n} = \frac{S_n}{n}.\)

Zaujíma nás či

\[P\left(S_{200} \leq 500 \right) = P\left(\bar{X}_{200} \leq \frac{500}{200} \right) = P\left(\sqrt{200}\frac{\bar{X}_{200}-2.3}{2} \leq \sqrt{200}\frac{2.5-2.3}{2} \right)\]

\[ \approx P(Z \leq \sqrt{2}) = \Phi(\sqrt{2}) = 92.13\%.\]

Cvičenie 9.11

Po 11 týždňoch bude v zásobníku

\(H = 74000 + X_1 + \cdots + X_{11} - (Y_1 + \cdots + Y_{11}) = 74 000 + S_{11} - T_{11}.\)

kde

\(X_1 = 47 000\) a \(\text{sd}[X_1] = 0.\)

\(Y_1 = 50 000\) a \(\text{sd}[Y_1] = 10 000.\)

\[P\left(H \leq 20 000 \right) = P\left(74 000 + 11 \cdot 47 000 - T_{11} \leq 20 000 \right) = P(T_{11} \geq 571 000)\]

\[P\left(\frac{T_{11}}{11} \geq \frac{571 000}{11}\right) = P\left(\sqrt{11}\frac{\bar{Y}_{11} - 50 000}{10 000} \geq \sqrt{11}\frac{\frac{571 000}{11} - 50 000}{10 000}\right) \]

\[\approx P\left(Z \geq 0.633\right) = 1-\Phi(0.633) = 26.3\%\]

Musíme nájsť \(D\) také, aby

\[P\left(H \leq 20 000 \right) = P\left(74 000 + 11 \cdot D - T_{11} \leq 20 000 \right) \leq 0.005.\] \[P\left(\frac{T_{11}}{11} \geq \frac{54 000 + 11D}{11}\right) = P\left(\sqrt{11}\frac{\bar{Y}_{11} - 50 000}{10 000} \geq \sqrt{11}\frac{\frac{54 000 + 11D}{11} - 50 000}{10 000}\right) \] \[\approx P\left(Z \geq \sqrt{11}\frac{\frac{54 000 + 11D}{11} - 50 000}{10 000}\right) \] Pretože \(\Phi(2.575) \approx 0.995,\)

potrebujeme aby

\[\sqrt{11}\frac{\frac{54 000 + 11D}{11} - 50 000}{10 000} > 2.575\]

Elementárnymi úprávami dosavame, že \(D > 52856.56\).